Below the margin of error

“a policy which recognises that individuals are the owners of their own lives, and which probably has the potential to win broad support at a time when they’re polling below the margin of error” – NZ Classic Liberal

“Radio Rhema, Inferno, Solid Gold, Radio Live, Sunday News,  and Herald On Sunday all rate below the margin of error” – Greater Queenstown/Arrowtown Media Survey

“Whether our party does well, or remains mired below the margin of error, there is little doubt that libertarian ideas are slowly diffusing into the public consciousness.” – Sean Fitzpatrick, Libertarianz

“Given that ACT was last polling below the margin of error, their opinions, flattering or otherwise, hardly seem likely to sway the result.” – The Northland Age.

“Look at Huntsman running below 2 percent. He is running below the margin of error. That’s how bad he’s doing. He may actually have zero or owe somebody votes.” – Dean Obeidallah

Dean Obeidallah is a professional comedian, and he knows it’s a joke.  The others seem to be serious, though they may just mean “very small” rather than anything more precise.

Careful pollers refer to the uncertainty margin they routinely quote as the “maximum margin of error”.  Unfortunately the first word gets left off by most people who quote the results.   The maximum margin of error in a poll is the margin of error in an estimate of 50%.   That’s fine for the major parties, but if you want to know how many people support Winston Peters, or how many believe they have been abducted by aliens, you need a different formula.

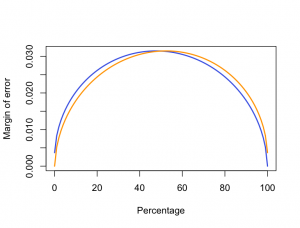
Since proportions can’t be negative, and since any non-zero percentage in a poll implies a non-zero percentage in the population, the uncertainty must be smaller for percentages near zero or one hundred.  The uncertainty range must also be asymmetric: a 1% result can’t overestimate the truth by more than 1%, but it could underestimate the truth by more than 1%.

The graph shows the upper (blue) and lower (orange) margins of error for percentages from 0 to 100% in a poll of 1000 people, the size that Colmar Brunton typically uses.  Over the range from about 20% to 80% the curve is pretty flat, and using the maximum margin of error is a good approximation.  For values less than 10% or more than 90% we need a better rule of thumb.

Some rough approximations that might be useful:

• At 10%, the margin of error is about two-thirds of the maximum
• At 5%, the crucial MMP threshold, the margin of error is about half the maximum
• For percentages greater than zero but less than the maximum margin of error, the relative margin of error is roughly 50%
• If the percentage is zero there isn’t any margin of error downwards, but the upper margin of error is 3 divided by the sample size (eg 3/1000=0.3% for a sample of 1000).

The first two of these rules of thumb come from the formula for the variance  of a proportion p, which is p(1-p)/n for a sample size of n. The maximum margin of error is the square root of 1/n, so we can work out n easily.

The last rule is the famous rule of three: if you see none of something, the upper bound for the proportion is the same as the estimate if you had seen three of them.

The third rule is a rough approximation based on looking at some numbers, and is less accurate than the others.