Posts written by James Russell (4)

David Whitehouse through the Global Warming Policy Foundation has recently released a report stating that “It is incontrovertible that the global annual average temperature of the past decade, and in some datasets the past 15 years, has not increased”. In case it is unclear, both the author and institute are considered sceptics of man-made climate change.

The report focuses on arguing the observation that if you look at only the past decade then there is no statistically significant change in global average annual temperature. Understanding what this does, or doesn’t, mean requires considering two related statistical concepts; 1) significant versus non-significant effects and 2) sample size and power.

Detecting a change is not the same as detecting no change. Statistical tests, indeed most of science, generally operates around Karl Popper’s falsification. Null hypotheses are set-up, generally a statement or test of the form ‘there is no effect’ and the alternative hypothesis is set-up in the contrary ‘there is an effect’. We then set-out to test these competing hypotheses. What is important to realise, however, is that technically one can never prove the null hypothesis, only gather evidence against it. In contrast however one can prove the alternative hypothesis. Scientists generally word their results VERY precisely. As a common example, imagine we want to show there are no sharks in a bay (our null hypothesis). We do some surveys, and eventually one finds a shark. Clearly our null hypothesis has been falsified, as finding a shark proves that there are sharks in the bay. However, let’s say we do a number of surveys, say 10, and find no sharks. We don’t have any evidence against our null hypothesis (i.e. we haven’t found any sharks..yet), but we haven’t ‘proven’ there are no sharks, only that we looked and didn’t find any. What if we increased it to say 100 surveys? That might be more convincing, but once again we can never prove there are no sharks, only demonstrate that after a large number of surveys (even 1,000, or 1,000,000) its highly unlikely there are any. In other words, as we increase our sample size, we have more ‘power’ (a statistical term) to be confident that they represent the underlying truth.

And so in the case of David Whitehouse’s claim we see similar elements. Just because an analysis of the last decade of global temperatures does not find a statistically significant trend, does not prove there is none. It may mean there has been no change, but it might also mean that the dataset is not large enough to detect it (i.e. there is not enough power). Furthermore, by reducing your dataset (i.e. only looking at the last 10 years rather than 30) you are reducing your sample size, meaning you are MORE likely NOT to detect an effect. A cunning statistical sleight of hand to make evidence of a trend disappear.

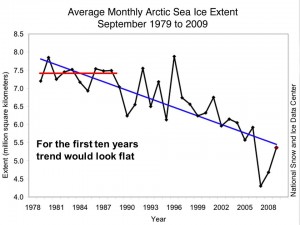
I lecture these basic statistical concepts to my undergraduate class and demonstrate it graphically. If you put a line over any ten years of data, it probably could be flat, only once you accumulate enough data, say thirty years, does the extent of the trend become clear.

Demonstrates the difficulty in detecting long-term trends with noisy data

This point is actually noted by the report (e.g. see Fig. 16).

Essentially, the only point that the report makes is that if you look at a small part of the dataset (less than a few decades), you can’t make a statistically robust conclusion, since you will be within a low power margin of error. Most importantly, we must be able to detect trends early even when the power to detect them may be low. And as I have stated in earlier posts, changes in variability are as important a metric as changes in the average, and the former, which is predicted from climate change, will make detecting the latter, which is also predicted, even more difficult.

The United States National Oceanic and Atmospheric Administration (NOAA) released a usual monthly State of the Climate Global Analysis in October 2012 which was anything but usual. Buried in the report was this astounding factoid: “This is the 332nd consecutive month with an above-average temperature”. What that means is, if you’re 27 or younger, you’ve never experienced a colder-than-average month. I find that phenomenal, a trend which if it continues might allow many to become ‘old timers’ who can “recollect the ‘good old days’ when a monthly temperature could be below average” (i.e. prior to March 1985).

This statement is certainly headline-grabbing, although there is some devil in the detail. Specifically, what is the ‘average’ which the NOAA benchmark against? A bit of research reveals that the NOAA use a reasonably robust 3-decade (1981-2010) average for their graphics, but the phrasing of the paragraph in question suggests that in this case they are comparing to the 20^th century average. If it was the 3-decade dataset then the months Jan 1981 – Feb 1985 would have had to have been exceptionally cold to skew the average so low that it could be exceeded 332 times consecutively.

The field of time series and calculating moving averages (and variabilities) is fascinating, and no doubt with sufficient data-mining, as in any field (imagine sporting statistics), a number of other shocking statistics could be extracted. Nonetheless a 332 month run is still impressive (or incredibly concerning). Interpretation of climate change will more and more require punters to be comfortable with interpreting both running averages and changing variabilities. We can have extremely cold snaps in a month (variability) while still having an above average month for temperature.

The New Zealand Medical Journal has this month published a review of cycling deaths in New Zealand, with the key finding being that “the helmet law has failed in aspects of promoting cycling, safety, health, accident compensation, environmental issues and civil liberties”. This is a bold claim which should be held to high scrutiny.

The journal article (accessible only by subscription, which we at the University of Auckland are fortunate enough to have) is available at the journal’s website, but for those without subscription access can only be to the media reports of it such as on Stuff.

The article itself is jam-packed full of statistics from various sources, so please bear with me.

The most important is probably Table 1, which shows that whereas pedestrian hours have remained relatively constant from 1989 to 2009, cycling hour have decreased by half, and Table 2, which shows that both pedestrian AND cyclist deaths have decreased from 1989 to 2009. Whereas both have gone down by half, the ratio has remained constant at about one quarter. However these statistics are then ‘corrected’ for the number of hours walked or cycled.

Given that cycling hours have significantly decreased by about 50%, as have the number of cycling deaths by 50% over the same period, the stark result is that cycling deaths per hour cycled have remained about constant over the study period – and certainly not evidence that the introduction of the helmet law, or any other event, has increased the accident rate. Something else is going on with pedestrian deaths altogether, which have encouragingly decreased substantially per walking hour over 1989-2009.

However, the author places emphasis on a new statistic – the ratio of cycling to pedestrian deaths. Whereas pedestrian deaths per hour have markedly gone down, cyclist deaths per hour have not. The ratio of the two means that cycling deaths have apparently increased (but importantly, only relative to pedestrian deaths).

The pedestrian deaths trend is actually a red herring, as we could well compare cycling deaths to any number of trends. According to Statistics New Zealand crime has also gone down since 1994. We could equally posit that the number of cycling deaths relative to crimes has increased, but would this be an alarming statistic? (are the criminals using bicycles as getaway vehicles?).

The article is also loaded with other fascinating statistical statements such as “that life years gained by cycling outweighed life years lost in accidents by 20 times”, which I will not cover the moral implications of here, but is that supposed to be some solace?

The key result from this study seems to in fact be that the rate of accidents for pedestrians has declined significantly over the period of the review, which has to be good news, especially prior to correction for population growth. That cycling hours have halved may well reflect increased awareness of the dangers of cycling in New Zealand.

Regardless of that main finding, the article commits one of the deadly sins of statistics, implying causation from correlation. That the helmet law was introduced in 1994 is about as relevant as TV2 beginning 24 hour programming, or the Winebox enquiry, both in that same year. We could compare trends before and after but with no experimental relationship between the process and the pattern, as tantalising as a relationship between bike helmet laws and accidents might be, it is only a correlation.

According to the Dominion Post Environment Minister Nick Smith said the clean-up effort and the reduced number of dying birds was encouraging, with regards to New Zealand’s worst environmental disaster with the grounding of Rena on the Astrolabe Reef.

Although at first glance a reduced number of dying birds may appear to be a good thing, the underlying process driving this trend is not clear. It could be that most birds at risk to the oil spill have already died, and the reduced number of dying birds is in fact because there are no more birds alive left to die.

Statistically, what are confounded here are the population size and the probabilities of detection and impact (from the oil spill). When the total number of birds being found dead has declined, we don’t know if the population size has remained relatively stable, but the number being detected and impacted has declined, or if the population size has declined, but the number being detected and impacted has remained constant. In both cases the calculation of the absolute number of birds being recovered comes out the same, but under the first scenario, the impact of the oil spill has declined, whereas in the second, the oil spill is having the same impact.

I hope for the sake of the birds it is the first scenario, as Nick Smith hopes, because as Minister of Conservation Kate Wilkinson says, “it’s not their fault.”