Posts written by Thomas Lumley (2534)

• Michael Neilson and Chris Knox at the NZ$ Herald have an excellent look at crime statistics and what you can’t straightforwardly conclude from them
• Outsourcing:  there was a story about garlic to stop Covid.  Here are responses from a blog at the University of Waikato, and from misinformation.wiki
• Many French labour regulations start to apply when you have 50 employees, says the Economist, showing the graph on the right that has a big drop in the number of businesses reporting 50 or more employees
  
  The graph on the left shows the same self-reporting from a different source.  The graph in the middle shows actual numbers of employees estimated using payroll data, with nothing happening at 50 — an interesting difference (from)

From Newshub: New study into therapeutic cannabis finds 96pct of participants report benefits in medical conditions.

This is deeply unsurprising, as I pointed out when similar results came out in 2017.  People who keep on using cannabis therapeutically are likely to think it works, because otherwise they wouldn’t.

This research, reported at Newshub, is pretty good: dogs are being evaluated for detecting Covid in reasonably large numbers of people at schools, and the results are actually published in a respectable peer-reviewed journal.  The numbers are still getting oversold a bit:

The study said [the dogs] were 83 percent accurate at identifying COVID-19-positive students, and 90 percent on the mark at picking out virus-negative students.

There are two issues here. First, 90% accuracy on virus-negative students is not at all good.  The current prevalence of Covid in NZ is maybe 1%, and the idea of dog-based-testing is for the subset of people who are possibly infected but apparently healthy, which will cut the numbers further.  Most of the people who test positive will be false positives, who will then need to be isolated for further testing.   Antigen tests have an accuracy in uninfected people (specificity) more like 99%.

Achieving 83% accuracy for identifying actual infections sounds good, and I’ve seen social media comments that it’s better than the antigen tests. It isn’t really: as the story says, the accuracy figure measures how well the dogs agree with the antigen tests.  83% accuracy means that the dogs are missing 17% of the infections that the antigen tests pick up.

If your school was doing regular testing of all students, this study suggests that you could reduce the amount of testing by using dogs to screen people first and only testing the kids who the dogs select. The accuracy would be lower than testing everyone, but it might be cheaper.   The study doesn’t really argue that dogs would be good on their own.

The story goes on to say

Dogs have also been using their powerful noses to detect other diseases such as cancer with shockingly high accuracy. 

Again, this is true (at least in a sense). Research studies, mostly small, have reported results of this sort for years. The fact that we aren’t currently using dogs to screen for any of these diseases suggests either that there are practical barriers to implementation, or that it doesn’t actually work all that well in practice.

From Ars Technica

An analysis of 2,007 damaged or defective hard disk drives (HDDs) has led a data recovery firm to conclude that “in general, old drives seem more durable and resilient than new drives.”

If you go out and lo0k at human deaths over a period of years, you will also find that Baby Boomers are much more likely die over age 70 than Gen X, and Gen X are more likely to die after 50 than millennials.  It’s too late for Boomers to die young.

Going on, we see that

backup and cloud storage company Backblaze uses hard drives that surpass the average life span Secure Data Recovery saw among the HDDs clients sent it last year. At the end of 2022, Backblaze’s 230,921 hard drives had an average age of 3.6 years versus the 2-year, 10-month average time before failure among the drives Secure Data Recovery worked on last year.

Again, if you look at an older group of people, the average age at death will be older than if you use a younger group.

This all wouldn’t matter so much, except that they are also trying to draw conclusions about novel disk drive technologies being less reliable.  There are statistical techniques to account for the different follow-up time of different groups of drives, but it’s quite possible those techniques would just tell you “nope, too soon to tell”.

There’s a 1News headline Only 1 in 4 Aucklanders back Wayne Brown’s sweeping cuts

I was expecting this to be based on proportions supporting the cuts in public submissions, but I was glad to see that the Council commissioned a proper survey in addition to accepting general comments and 1News reported it correctly.  That’s an excellent combination: open public comment allows people to point out problems or solutions you haven’t considered and a survey allows quantitative measurement for issues where you know the options in advance. More organisations should do this.

As you’d expect, trying to get quantitative results from the public comment doesn’t work very well. For example, 1News reported that 40% of submitters didn’t want any cuts, as opposed to the estimate of 7% for all Auckland in the survey.  People who have something to say are more likely to say it.

The number of submissions was very large: more than 10% of the number of votes in the mayoral election.  Even so, the submissions are very unrepresentative. That’s not a problem if you aren’t trying to get quantitative results; having the input biased towards experts and people who care a lot can be helpful.  It would be a problem if you were just counting the results.

Stuff has an important report on road injuries in Auckland, based on a review by Auckland Transport (that doesn’t seem to be available).   They looked at the numbers of serious injuries over three years, both as reported by the police crash analysis system and as reported by the hospitals where the people turned up for treatment. These numbers were not the same

Even the discrepancy for cars is a bit surprising: ‘serious injuries’ here mean hospital admission (an overnight stay).  It’s not clear whether the police are missing half the serious-injury crashes or under-reporting how many people end up in hospital, but I would have expected more completeness of reporting for hospitalisation of people in vehicles. (According to the law, even accidents involving bikes or e-scooters without cars  that result in injury have to be reported to the police, but I’m less surprised this doesn’t happen.)

Some of the bike and pedestrian and ‘transport device’ injuries that are being missed will be crashes that didn’t involve cars.  That’s the dashed/solid distinction in the graph. The data match international research on e-scooter crashes suggesting that most injuries are to the rider, and so may be relatively less likely to get reported to police.  For bikes, a potentially worrying category is injuries involving stationary cars — ‘doorings’ — which might be less likely to get reported than those involving moving cars.

Another important concern, though, is the definition of ‘serious injury’. An injury causing broken bones and resulting in weeks or months of significant disability, but not involving an overnight hospital stay, would not be meet the threshold.  This implies even the MoH statistics are also missing a lot of injuries that a normal person would call ‘serious’.

Turnitin, a company that looks for similar word sequences in student assignments, says that it can now detect ChatGPT writing.  (Stuff, RNZ)

The company is 98% confident it can spot when students use ChatGPT and other AI writing tools in their work, Turnitin’s Asia Pacific vice president James Thorley said.

“We’re under 1% in terms of false positive rate,” he said.

It’s worth looking at what that 1% actually means.  It appears to mean that of material they tested that was genuinely written by students, only 1% was classified as being written by ChatGPT.  This sounds pretty good, and it’s a substantial achievement if it’s true. This doesn’t mean that only 1% of accusations from the system are wrong. The proportion of false accusations will depend on how many students are really using ChatGPT. If none of them are, 100% of accusations will be false; if all of them are, 100% of accusations will be true.

What does the 1% rate mean for a typical student?  An average student might hand in 4 assignments per course, for 4 courses per semester, two semesters per year.  That’s nearly 100 assignments in a three-year degree.  A false accusation rate of 1 in 100 means an average of one false accusation for each innocent student, which doesn’t sound quite as satisfactory.

The average is likely to be misleading, though.  Some people will be more likely than others to be accused.  In addition to knowing the overall false positive rate, we’d want to know the false positive rate for important groups of students.  Does using a translator app on text you wrote in another language make you more likely to get flagged? Using a grammar checker? Speaking Kiwi? Are people who use semicolons safe?

Turnitin emphasize, as they do with plagiarism, that they don’t want to be blamed for any mistakes — that all their tools do is raise questions.  For plagiarism, that’s a reasonable argument.  The tool shows you which words match, and you can then look at other evidence for or against copying. Maybe the words are largely boilerplate. Maybe they are properly attributed, so there is copying but not plagiarism.  In the other direction, maybe there are text similarities beyond exact word matches, or there are matching errors — both papers think Louis Armstrong was the first man on the moon, or something.  With ChatGPT there’s none of this. It’s hard to look for additional evidence in the text, since there is no real way to know whether something you see is additional or is part of the evidence that Turnitin already used.

• How to win at roulette. No, they haven’t repealed the martingale optional stopping theorem, but no mathematical model is a perfect description of reality
• Farah Hancock has a good series of reports about Auckland and Wellington buses, for Radio NZ.
• “At the outset, it’s important to note that the finding that “exercise is better than medicine” for depression is one that you cannot possibly make from this paper, because the authors *literally excluded papers that compared exercise to medication*” — a Twitter thread on claims about a new study
• Riding an electric bike drops heart and cancer risks, finds German study. Except it doesn’t.  The published German study compares exercise levels and accident rates of a group of people riding electric and acoustic bikes. That’s all it does. Unsurprisingly, it finds that the e-bikers still get exercise, but not quite as much as the people using traditional bicycles.  There’s a lot of claims of evidence of major  health effects, that the researchers are supposed to have described to Der Spiegel (I don’t subscribe, so I can’t check).  These are (a) unpublished, and (b) can’t be as described — the study included about 2000 reasonably healthy participants and ran for twelve months, so it can’t possibly have collected substantial evidence about prevention of cancer or Alzheimer’s or heart disease.  That’s before we even get to any issues about confounding: how much does your health affect cycling vs cycling affecting your health.  As a long-term e-cyclist, I’d love these claims to be based on convincing evidence, but they just aren’t.
• Via David Rumsey on Twitter, the first ‘flow’ visualisation maps, from the 1838 Irish Railway Commission Atlas
• 
• From Kieran Healy, the relationship between height and number of points scored in the US professional basketball league. No, there isn’t a visually clear relationship. That’s because you’re selecting everyone for being very good at basketball, and the shorter guys need to be better in other ways to compensate.  Height obviously matters; other things matter too.  In the same ways, using some sort of standardised test as a criterion for university admission will make it look as if the test isn’t related to performance at university.
  

From Stuff: Japan just found 7000 islands it never knew existed

That’s not quite what happened, as the story goes on to say.  We’re not talking about Kupe discovering Aotearoa or even Abel Tasman ‘discovering’ New Zealand.  There are three main groups of ‘new’ islands:

• Pairs or small groups of islands that were counted as a single island before and are now recognised as multiple separate islands.
• Islands in rivers or lakes, which were known about before but not part of the previous count
• Large sandbars, which were known about before, but used not to be included in the definition of ‘island’

There are also islands genuinely appearing and disappearing, because of volcanic activity and erosion, but that’s a tiny fraction of the discrepancy.

Counting things requires both a definition of the thing to be counted and good enough measurement to see and recognise them.  In other news, the New Zealand Census is on!

There’s been a scary news story about an artificial sweetener that previously looked remarkably inoffensive, erythritol.  It’s produced by fermentation of various plant material, and it comes in ‘organic’ as well as normal versions; it’s got similar taste and feel to sugar, and you can even use it for baking.  So when someone reports that it increases the risk of heart attack by a lot, you’d hope they had investigated thoroughly.

The researchers didn’t particularly have it in for erythritol; they were looking at blood components to see if anything predicted heart attack by a useful amount, and found a dramatic correlation with the amount of erythritol in the blood — and I mean dramatic. Here’s the chart showing the percentage of people who didn’t have a heart attack over the three years after their blood measurement, divided into four equal groups based on erythritol in the blood:

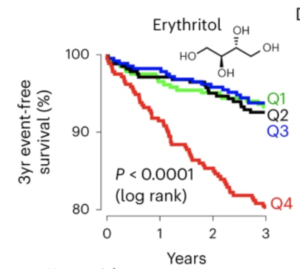
It’s not quite as bad as it first looks — the y-axis only goes down to 80% — but it still suggests more than half of heart attacks are due to erythritol, making it almost as bad as smoking. And also that there’s a magic threshold between safe and dangerous doses. This is … hard to believe? Now, this was the group where they discovered the correlation, so you’d expect over-estimation.  Not being completely irresponsible, they did check in other groups of people. Here’s a separate US group

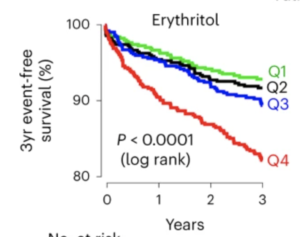
It’s not quite as dramatic, but we’re still looking at a doubling of risk in the highest group and no real difference between the other three. And we’re still looking at nearly half of heart attacks being due to this obscure artificial sweetener.

So it is credible?

One question to ask is whether there’s a mechanism for it to be dangerous — this isn’t a definitive criterion, because there’s a lot we don’t know, but it’s useful.  The researchers say that erythritol makes platelets more likely to clump together, triggering clots, which is a thing that can happen and would increase heart attack risk — that’s why aspirin, which disables platelets, has been recommended to prevent heart attacks.

Another question to ask is whether the high erythritol group got it from eating the most erythritol. If they aren’t, this isn’t going to give useful dietary advice.  The compound is made in the body to some extent, and it’s excreted via the kidneys. Could people at higher risk of heart attack be making more internally or excreting it less effectively?  The natural step here would be to feed healthy people some erythritol and see what happens to their platelets.  That study is apparently underway, though it’s small and has no control group.

You might also ask if there has been a dramatic increase in heart attacks over the time that erythritol has become more popular in foods?  There hasn’t been, though a moderate increase might have been masked by all the other factors causing decreases in risk.

I would be surprised if the risk turns out to really be this big, though it’s entirely possible that there’s some risk. At least the platelet study should be reasonably informative, and it’s a pity it wasn’t done before the publicity.