Bell curves, bunnies, and dragons
Keith Ng points me to something that’s a bit more technical than we usually cover here on StatsChat, but it was in the New York Times, and it does have redeeming levels of cutesiness: an animation of the central limit theorem using bunnies and dragons
The point made by the video is that the Normal distribution, or ‘bell curve’, is a good approximation to the distribution of averages even when it is a very poor approximation to the distribution of individual measurements. Averaging knocks all the corners off a distribution, until what is left can be described just by its mean and spread.
The central limit theorem is absolutely vital to statistics, since it (and more advanced versions) say that even if the distribution of your data is complicated, the distribution of the summaries you care about (eg mean or median) is often close to a simple Normal distribution. Lots of scientists don’t really appreciate the central limit theorem, and even statisticians often don’t realise how well it works. Here is an example that’s less cute than the bunnies but more dramatic. The graph shows a probability distribution for individual measurements (top left) and then for averages of 5, 10, or 20 measurements, each with a superimposed bell curve
The individual observations are nowhere near the Normal distribution, but averaging over a sample of even 5 observations gives something much closer to the bell curve, and the average of 10 or 20 observations is almost a perfect fit.
Together with some colleagues in Seattle I wrote a scientific paper about this, primarily so we had something to point to when scientists asked us “But is there a reference?”
Thomas Lumley (@tslumley) is Professor of Biostatistics at the University of Auckland. His research interests include semiparametric models, survey sampling, statistical computing, foundations of statistics, and whatever methodological problems his medical collaborators come up with. He also blogs at Biased and Inefficient See all posts by Thomas Lumley »
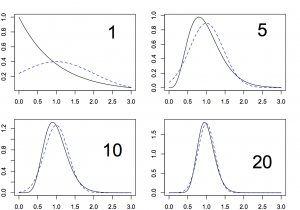
These are averages of random samples in the distribution?
11 years ago
Yes. Well, no. Well, yes.
They are the exact distributions of averages of random samples from the distribution. However, they aren’t obtained by actually taking random samples and averaging, but by working out the distribution mathematically.
11 years ago