Posts written by James Curran (32)

Watch Ross Ihaka talk to Ximena Smith about R and other things:

https://www.teaomaori.news/statistics-legend-ross-ihaka-reflects-on-his-revolutionary-software

In early May we received the fantastic news that fellow New Zealander Professor Bruce Weir, who is an Honorary Professor at the University of Auckland as well as a Professor of Statistical Genetics at the University of Washington, has been elected to the prestigious position of Fellow of the Royal Society.

Our NZSA colleague, Dr Harold Henderson, sent members a link to a feature article in Stuff which we thought StatsChat readers may enjoy.

NPR’s Planet Money ran an interesting podcast in mid-January of this year. I recommend you take the time to listen to it.

The show discussed the idea that there are problems in the way that we do science — in this case that our continual reliance on hypothesis testing (or statistical significance) is leading to many scientifically spurious results. As a Bayesian, that comes as no surprise. One section of the show, however, piqued my pedagogical curiosity:

STEVE LINDSAY: OK. Let’s start now. We test 20 people and say, well, it’s not quite significant, but it’s looking promising. Let’s test another 12 people. And the notion was, of course, you’re just moving towards truth. You test more people. You’re moving towards truth. But in fact – and I just didn’t really understand this properly – if you do that, you increase the likelihood that you will get a, quote, “significant effect” by chance alone.

KESTENBAUM: There are lots of ways you can trick yourself like this, just subtle ways you change the rules in the middle of an experiment.

You can think about situations like this in terms of coin tossing. If we conduct a single experiment where there are only two possible outcomes, let us say “success” and “failure”, and if there is genuinely nothing affecting the outcomes, then any “success” we observe will be due to random chance alone. If we have a hypothetical fair coin — I say hypothetical because physical processes can make coin tossing anything but fair — we say the probability of a head coming up on a coin toss is equal to the probability of a tail coming up and therefore must be 1/2 = 0.5. The podcast describes the following experiment:

KESTENBAUM: In one experiment, he says, people were told to stare at this computer screen, and they were told that an image was going to appear on either the right site or the left side. And they were asked to guess which side. Like, look into the future. Which side do you think the image is going to appear on?

If we do not believe in the ability of people to predict the future, then we think the experimental subjects should have an equal chance of getting the right answer or the wrong answer.

The binomial distribution allows us to answer questions about multiple trials. For example, “If I toss the coin 10 times, then what is the probability I get heads more than seven times?”, or, “If the subject does the prognostication experiment described 50 times (and has no prognostic ability), what is the chance she gets the right answer more than 30 times?”

When we teach students about the binomial distribution we tell them that the number of trials (coin tosses) must be fixed before the experiment is conducted, otherwise the theory does not apply. However, if you take the example from Steve Lindsay, “..I did 20 experiments, how about I add 12 more,” then it can be hard to see what is wrong in doing so. I think the counterintuitive nature of this relates to general misunderstanding of conditional probability. When we encounter a problem like this, our response is “Well I can’t see the difference between 10 out of 20, versus 16 out of 32.” What we are missing here is that the results of the first 20 experiments are already known. That is, there is no longer any probability attached to the outcomes of these experiments. What we need to calculate is the probability of a certain number of successes, say x given that we have already observed y successes.

Let us take the numbers given by Professor Lindsay of 20 experiments followed a further 12. Further to this we are going to describe “almost significant” in 20 experiments as 12, 13, or 14 successes, and “significant” as 23 or more successes out of 32. I have chosen these numbers because (if we believe in hypothesis testing) we would observe 15 or more “heads” out of 20 tosses of a fair coin fewer than 21 times in 1,000 (on average). That is, observing 15 or more heads in 20 coin tosses is fairly unlikely if the coin is fair. Similarly, we would observe 23 or more heads out of 32 coin tosses about 10 times in 1,000 (on average).

So if we have 12 successes in the first 20 experiments, we need another 11 or 12 successes in the second set of experiments to reach or exceed our threshold of 23. This is fairly unlikely. If successes happen by random chance alone, then we will get 11 or 12 with probability 0.0032 (about 3 times in 1,000). If we have 13 successes in the first 20 experiments, then we need 10 or more successes in our second set to reach or exceed our threshold. This will happen by random chance alone with probability 0.019 (about 19 times in 1,000). Although it is an additively huge difference, 0.01 vs 0.019, the probability of exceeding our threshold has almost doubled. And it gets worse. If we had 14 successes, then the probability “jumps” to 0.073 — over seven times higher. It is tempting to think that this occurs because the second set of trials is smaller than the first. However, the phenomenon exists then as well.

The issue exists because the probability distribution for all of the results of experiments considered together is not the same as the probability distribution for results of the second set of experiments given we know the results of the first set of experiment. You might think about this as being like a horse race where you are allowed to make your bet after the horses have reached the half way mark — you already have some information (which might be totally spurious) but most people will bet differently, using the information they have, than they would at the start of the race.

Dan Kopf from Priceonomics has written a nice article about one of Auckland’s famous graduates, Hadley Wickham. The article can be found Hadley Wickham.

Gareth Robins has answered this question with a very beautiful visualization generated with a surprisingly compact piece of R code.

Distance to the nearest road in New Zealand

Check out the full size image and the coded here.

A nice animated GIF showing what difference a small amount of simple formatting can make to a simple table. You may need to click on the image.

Just a quick pointer to a nice opinion piece by the Financial Times’ “Undercover Economist” and star of BBC Radio 4’s excellent “More or Less” podcast, Tim Harford. Tim very nicely argues that in the hype over big data, stories of the failures of simplistic, correlation driven approaches rarely get airtime, and hence we get a misleading impression about the efficacy of these techniques.

It was with some amazement that I read the following in the NZ Herald:

Since his first test in charge at Cape Town 13 months ago, McCullum has won just five out of 13 test tosses. Add in losing all five ODIs against India and it does not make for particularly pretty reading.

Then again, he’s up against another ordinary tosser in MS Dhoni, who has got it right just 21 times out of 51 tests at the helm. Three of those were in India’s past three tests.

The implication of the author seems to be that five out of 13, or 21 out of 51 are rather unlucky for a set of random coin tosses, and that the possibility exists that they can influence the toss. They are unlucky if one hopes to win the coin toss more than lose it, but there is no reason to think that is a realistic expectation unless the captains know something about the coin that we don’t.

Again, simple application of the binomial distribution shows how ordinary these results are. If we assume that the chance of winning the toss is 50% (Pr(Win) = 0.5) each time, then in 13 throws we would expect to win, on average, 6 to 7 times (6.5 for the pedants). Random variation would mean that about 90% of the time, we would expect to see four to nine wins in 13 throws (on average). So McCullum’s five from 13 hardly seems unlucky, or exceptionally bad. You might be tempted to think that the same may not hold for Dhoni. Just using the observed data, his estimated probability of success is 21/51 or 0.412 (3dp). This is not 0.5, but again, assuming a fair coin, and independence between tosses, it is not that unreasonable either. Using frequentist theory, and a simple normal approximation (with no small sample corrections), we would expect 96.4% of sets of 51 throws to yield somewhere between 18 and 33 successes. So Dhoni’s results are somewhat on the low side, but they are not beyond the realms of reasonably possibility.

Taking a Bayesian stance, as is my wont, yields a similar result. If I assume a uniform prior – which says “any probability of success between 0 and 1 is equally likely”, and binomial sampling, then the posterior distribution for the probability of success follows a Beta distribution with parameters a = 21+ 1 = 22, and b = 51 – 21 + 1 = 31. There are a variety of different ways we might use this result. One is to construct a credible interval for the true value of the probability of success. Using our data, we can say there is about a 95% chance that the true value is between 0.29 and 0.55 – so again, as 0.5 is contained within this interval, it is possible. Alternatively, the posterior probability that the true probability of success is less than 0.5 is about 0.894 (3dp). That is high, but not high enough for me. It says there at about a 1 in 10 chance that the true probability of success could actually be 0.5 or higher.

There has been significant coverage in the press of New Zealand’s slip in the OECD PISA (Programme for International Student Assessment) rankings for mathematics, reading, and science.
We probably should be concerned.

However, today I stumbled across the following chart: 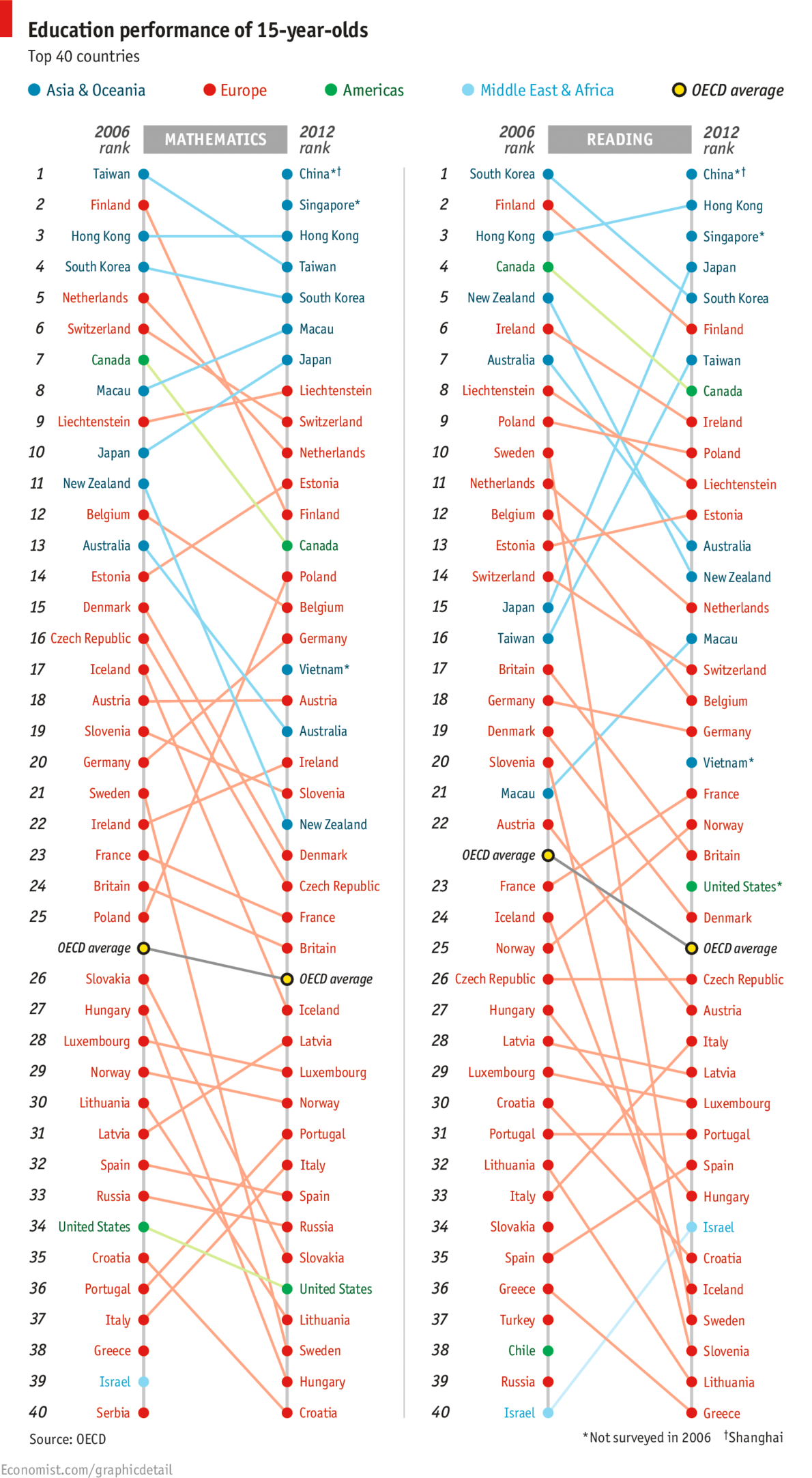in The Economist. Two things about it struck me. Firstly, part of the change (in the mathematics ranking at least) was driven by the addition of three countries/cities which did not participate in the 2006 round: Shanghai, Singapore, and Vietnam. The insertion of these countries is not enough to explain away New Zealand’s apparent drop, but it does move us from a change of down 11 places to a change of down 8 places. Secondly, I found it really hard to see what was going on in this graph. The colour coding does not help, because it reflects geographic location and the data is not grouped on this variable. Most of the emphasis is probably initially on the current ranking which one can easily see by just reading the right-hand ranked list from The Economist’s graphic. However, relative change is less easily discerned. It seems sensible, to me at least, to have a nice graphic that shows the changes as well. So here it is, again just for the mathematics ranking: .

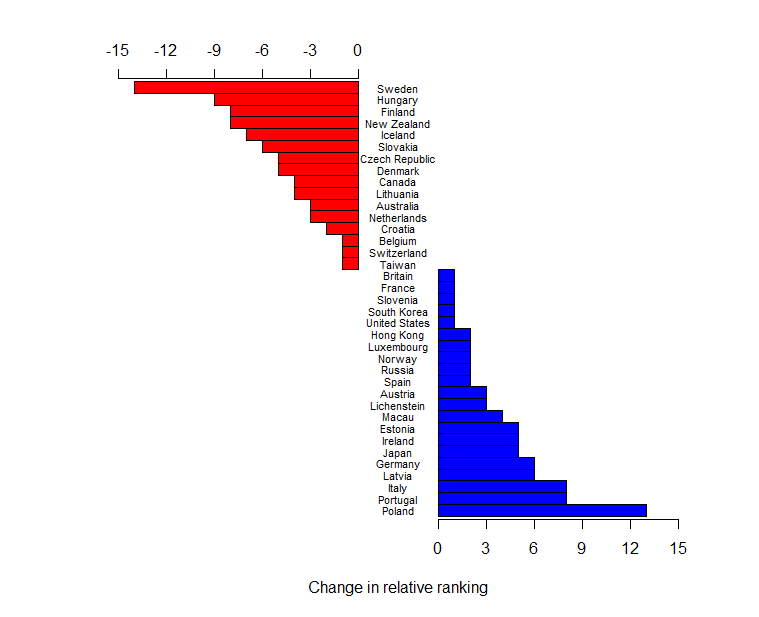The raw data (entered by me from the graph) has been re-ranked omitting Greece, Israel, and Serbia who did not participate in 2012, and China, Singapore, and Vietnam, who did not participate in 2006. I am happy to supply the R script to anyone who wants to change the spacing – I have run out of interest.

It is also worth noting that these rankings are done on mean scores of samples of pupils. PISA’s own reports have groups of populations that cannot be declared statistically significantly different (if you like to believe in such tests). This may also change the rankings.

Updates:

Professor Neville Davies, Director of the Royal Statistical Society’s Centre for Statistical Education, and Elliot Lawes, kindly sent me the following links:

Firstly a blog article from the ever-thoughtful Professor David Spiegelhalter: The problems with PISA statistical methods

and secondly, a couple of articles from the Listener, which I believe Julie Middleton has also mentioned in the comments:
Education rankings “flawed” by Catherine Woulfe” and Q&A with Andreas Schieicher also by Catherine Woulfe.

Anecdotally, many of the New Zealanders I talk to think that a) all American beer is appallingly bad, and that b) this is all that Americans drink. In fact, the US has been leading the micro- and craft- brewing revolution for some years now, and a new survey shows that American beer drinking tastes are changing. Budweiser, the so-called King of Beers, a product of US brewing giant Anheuser Busch, appears to have been deposed by Colorado based Blue Moon Brewing Company. I am sure someone will tell me that far more Budweiser/Millers/Coors is produced than beer from Blue Moon, but hey maybe American’s are just using it to pre-cook bratwursts before grilling like I used to do.

I was a little concerned that this study might be self-selected, or industry motivated, but the information provided gives some reassurance: “Data on behalf Blowfish for Hangovers by a third party, private research firm based on a study of 5,249 Americans who drink alcohol and are over the age of 21. Margin of error for this study is 1.35% at a 95% confidence interval. Additional data on alcoholic beverage sales collected directly by the Alcoholic Epidemiolic Data System (AEDS) from States or provided by beverage industry sources.”