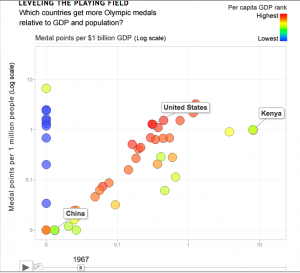
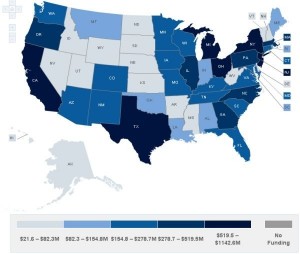
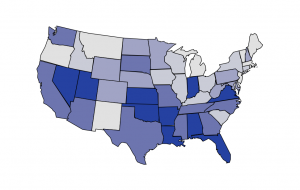
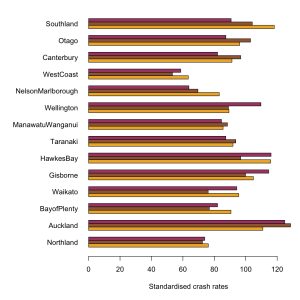
Numerate Queenstown police.
From the Otago Daily Times:
Over the weekend, police dealt with seven separate incidents involving Australians, including theft, nudity, disorderly behaviour and gross intoxication.
Sergeant Mark Gill said although the numbers appeared to show the Australians behaving badly, it was proportional to Queenstown’s Australian visitor ratio with other nationalities.
The common denominator in many small crimes in Queenstown’s CBD was too much alcohol and that was an issue for the police, Sgt Gill said.
Looking at the rest of his comments, Sgt Gill is clearly trying to stop Queenstown looking dangerous and scaring off tourists, but it’s encouraging whenever we see denominators being used sensibly in public by people who aren’t (as far as I know) trained professionals.